Gradient descent for multiple variables

Continue from the preceding example

[Ex]
$$\begin{array}{llll} \hfill\mathrm{Size~in~feet^2 (x_1)}\hfill & \hfill\mathrm{\#~bedrooms(x_2)}\hfill & \hfill\mathrm{\#~ floors(x_3)}\hfill & \hfill\mathrm{Age(x_4)}\hfill & \hfill\mathrm{Price~$1000~(y)}\hfill \\ \hline \\ 2104 & 5 & 1 & 45& 460 \\ 1416 & 3&2&40&232 \\ 1534 & 3&2&30&315 \\ 852 & 2&1&36&178 \\ ... & ...& ...& ...& ... \\ \end{array}$$

Notation:

• n = number of variables
• m = number of examples
• $x^{(i)}$ = input variables of  $i^{th}$ training example.
• $x^{(i)}_j$ = value of input variable j  in $i^{th}$ training example.

Hypothesis: $h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3 + \theta_4 x_4$

For convenience of notation, define $x_0 = 1$, it means $x^{(i)}_0 = 1$, so the hypothesis can transfer as:

$h_\theta(x) = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3 + \theta_4 x_4$

         $= \theta^T x$

So, the definition is as below:

[Def]
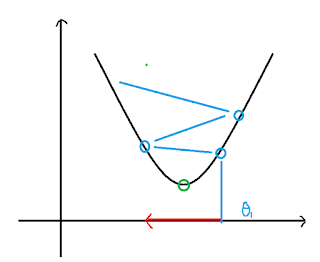
$$\begin{align*}& \text{repeat until convergence:} \; \lbrace \newline \; & \theta_j := \theta_j - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \; & \text{for j := 0...n}\newline \rbrace\end{align*}$$

Batch gradient descent

[Ex]
Continue from the preceding article about cost function, here we will use this method to minimize the cost function, and using just two parameters $\theta_0$ and  $\theta_1$ . It's a more general algorithm, and not only in linear regression.

outline:

• start with some  $\theta_0$ and  $\theta_1$ 
• keep changing the  $\theta_0$ and  $\theta_1$  to reduce the $J(\theta_0, \theta_1)$ and end up at a minimum

[Def]
repeat until converge {
$\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)$        (for j = 0 and j = 1)
}

$\alpha$ : learning rate, it means how big step we take with creating descent.
Each step of gradient descent uses ALL the training examples.

Notice: we need updating these parameters "simultaneously" !

[Ex]
Back to our example, we take one parameter $\theta_1$ now to get this algorithm more simpler.
[Plot 1]

Assuming this is our cost function, and if our  $\theta_1$ starting from the blue point, since the slope is positive, so the new $\theta_1$ from the gradient descent will decrease and  move to the green point (minimum), the moving speed depend on the $\alpha$. In contrast, if our  $\theta_1$ starting from the red point, it'll increase and move to the green point, too.

Although the moving speed is depend on the $\alpha$, when $\alpha$ is bigger the converging speed is more faster, but if the $\alpha$ is too big, the result will be diverging.
[Plot 2]

On the contrary, if the $\alpha$ is too small, it'll take too much time to converge.
[Plot 3]

Here is the other property of gradient descent, if our initial  $\theta_1$ is at the local optimum, then it leaves $\theta_1$ unchanged, because the slope will nearly equal to zero.
[Plot 4]

So, as we approach a local minimum, the gradient descent will automatically take smaller steps, this is why we don't need to decrease $\alpha$ over time.

[For linear regression]
[Def]
$$\frac{\partial}{\partial \theta_j}J(\theta_0,\theta_1) = \frac{\partial}{\partial \theta_j}\frac{1}{2m} \sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$$

$\begin{align*} \text{repeat until convergence: } \lbrace & \newline \theta_0 := & \theta_0 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m}(h_\theta(x_{i}) - y_{i}) \newline \theta_1 := & \theta_1 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m}\left((h_\theta(x_{i}) - y_{i}) x_{i}\right) \newline \rbrace& \end{align*}$

Cost Function

[Ex]
Here is our training set and hypothesis as below:
$$\begin{array}{ll} \hfill\mathrm{Size~in~feet^2 (x)}\hfill & \hfill\mathrm{Price($)~in~1000's(y)}\hfill \\ \hline \\ 2104 & 460 \\ 1416 & 232 \\ 1534 & 315 \\ 852 & 178 \\ ... & ... \\ \end{array}$$

In this example, we want to fit a straight line to predict the house price, then we set a simple model.
Hypothesis: $h_\theta(x) = \theta_0 + \theta_1 x$

It's a simple regression problem, you can choose any number for $\theta_0$ and $\theta_1$, so that we can get the $h_\theta(x)$ and it's meaning the value which the model predict to the input x. As a prediction model, we want the difference between $h_\theta(x)$ and y to be small, in other words
is this hypothesis good fit to the data?

We can measure the accuracy of our hypothesis function by using a cost function or called squared error function, in other words it's almost the same as MSE in statistics.

[Def]
$$J(\theta_0, \theta_1) = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left ( \hat{y}_{i}- y_{i} \right)^2 = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left (h_\theta (x_{i}) - y_{i} \right)^2$$
m: the number of training example
$h_\theta(x)$: form of hypothesis